Math Problem

[mattawajeep]

So, this isn't really important, it's just driving me nuts.

Was trying to draw my lot details in AutoCAD for house positioning and such and realized that I don't have all the info to get it in there exactly.




So, here's the problem:

You have a 4 sided polygon with known side lengths and the total area. No other information, no angles, diagonals nada.

Here's the polygon with the labeled sides and the area. Find the angles and diagonals.




I gave up after a full sheet of paper filled with numbers when I discovered that I couldn't remember how to solve a quadratic when x is to the 4th power.

... If any of my calculus classes ever actually covered it, it's been too long.

I'll give a hint, I'm thinking there are actually two possible real answers, and several unreal numbers.

[scumby]

why do you need diagonals? if you cut it into 2 triangles will that help? OR am i misunderstanding?

[SPR]

I like Al's answer. There must be an online calculator for this.

[Grumpy]

ftp://ftp.fao.org/fi/cdrom/fao_training ... 707e03.htm

[mattawajeep]

why do you need diagonals? if you cut it into 2 triangles will that help? OR am i misunderstanding?

Correct, partly. Cuttining it into triangles will make everything much easier, however, you'll need a diagonal to make the triangle useful. Which requires the use of Heron's Formula, at which point my math dissolved.

There are no online calculators for a polygon, but there are for triangles. It's a complexity issue and no one has bothered to write anything yet. Too many unreal possibilities which causes programming issues.

[SPR]

Does this look right?

[Jay W]

You are assuming the bottom left corner is a right angle. Nothing on the diagram can assure you of that.

[mattawajeep]

You are assuming the bottom left corner is a right angle. Nothing on the diagram can assure you of that.

Yup. That's what makes this problem entertaining. In the real world it doesn't matter, and a right angle would work, as it's so close. In the exact world however, it would change the area.

[Lud]

Ok I'll bite. What's the units of measurement for the sides?

[mattawajeep]

Ok I'll bite. What's the units of measurement for the sides?

Feet

[SPR]

Doesn't your plot description tell you the distance and the angles (degrees) for each corner?

[Lud]

I'll post up details. So far I have diagonals at 730.8388327121104 or about 730.84 ft. Hintyou need to use the perimeter and area which you already have. Just by looking at it those angles are pretty close to right angles meaning unless u have a pressing need for exact measurement I'd just do it Steve's way.

[Lud]

The four angles.

Top left 90.269 degrees

Top right 89.765 degrees

Bottom left 90.469 degrees

Bottom right 89.557 degrees

Diagonal of 730.84

I'm like 13 years removed from this stuff and I've worked 7 days in s row going on 8. This is my best stab at it.

[mattawajeep]

The four angles.

Top left 90.269 degrees

Top right 89.765 degrees

Bottom left 90.469 degrees

Bottom right 89.557 degrees

Diagonal of 730.84

I'm like 13 years removed from this stuff and I've worked 7 days in s row going on 8. This is my best stab at it.

I'm gonna plug this into the computer this evening and see how things come out, but it looks correct to me.

How'd you do it? Heron's formula or similar to come up with the triangle perimeter? I'm pretty sure I was on the right track, it was just the factoring that I couldn't remember how to do.

[pascoscout]

You'd have to factor out x to get to an equation that looked like ax^2+bx+c=0. Then use the quadratic equation solver.

Sorry to say but without the bearing of the top or bottom line I think this is an impossible solve. You cannot assume the top and bottom lines are parallel (note the 3 feet difference in the east and west lines) and looking at the east and west lines you will see that they are not parallel, this means at least one of the corner angles is not 90 degrees (as stated before). Assuming they are might get you close but not exact since the pythagorean theorem (a^2+b^2=c^2) only applies to right triangles.

To solve a triangle you need one of the following: All three angles, Two angles and a side, Two sides and an angle, all three sides. Having those you would use the law of sines, the law of cosines, or the Pythagorean theorem to get the remaining information. Without them there are an infinite number of solutions (aka unsolvable). Sine we cannot reasonably assume any of the angles is 90 degrees I don't see a way to calculate the diagonal. I suppose there might be a process of iterations to get to a solution, however, while you may come up with a solution that works it would only be one of an infinite number of correct solutions and not what actually exists in the real world. If you could get the bearing for at least the top or bottom line you could calculate one angle and problem solved.

Herons Formula could not be used as this a polygon (no parallel sides) and not a rectangle or parallelogram so you cannot assume that bisecting it with a diagonal would result in two halves with equal areas. i.e. the area of either triangle is unknowable without more information.

This appears to be a cut out from a full plat. Do you have the rest of the plat? A full copy should have come with your title report when you bought the place. If you don't have it do you at least have a legal description or the name of the plat that you could get a copy from the County Auditor? With your parcel number you can look it up on the assessors website (assuming Grant County?). Once you have the plat name you can look it up on their eagleweb and get a free copy of the document. That would give you the top and bottom angles then its a simple matter of entering them into autocad.. no math. If you have Civil 3D its draw line by bearing. If its plain old autocad there is a way to do but I'd have to do it at work tomorrow to recall. Its either @bearing<distance or @distance<bearing where the bearing is entered as Yzzdzz'zz"X (Y is north or south and X is east or west and z's are the actual measurement).

If it doesn't have to be exact just insert your image into autocad as a raster or OLE object and trace over it. Since you know at least one measurement you can scale it to nearly the correct size and be close.

If ya'd like some help shoot me a PM with your phone number.

[SPR]

That be an answer

[OldGreen]

That was my math wizard's explanation as well. You can use the law of cosines but you need 1 angle.

[Lud]

I didn't use the quadratic equation at all. There's a formula for calculating the diagonal or any shape using perimeter. After that it's simple trig functions. Remember this one?
SOHCATOA....sin=opposite/hypotenuse. Exc...use the sides of the newly found triangles and you work using cosecant cotangent ect to find the angles. Also all angles in any triangle add up to 180 degrees and in a rectangle like shape they add up to 360 degrees even if the angles aren't right angles like in your example.

[mattawajeep]

I didn't use the quadratic equation at all. There's a formula for calculating the diagonal or any shape using perimeter. After that it's simple trig functions. Remember this one?
SOHCATOA....sin=opposite/hypotenuse. Exc...use the sides of the newly found triangles and you work using cosecant cotangent ect to find the angles. Also all angles in any triangle add up to 180 degrees and in and rectangle like shape they add up to 360 degrees even if the angles aren't right angles like in your example.

How'd you come up with the diagonal so that you could get the perimeter though?

[Lud]

When I get home I'll look at the sheet of paper I used to write everything out. I used my old notes from college. You find the perimeter by adding up all the sides. You gave me the area too. I know theres a way to use area as well but I forgot all that stuff. They way I did it the lines do not need to be parallel. Note: I only found one diagonal. I'm not sure it is the exact same as the other. As stated before one cannot reasonably assume one diagonal bisects the figure the exact same as the other. Which is why I was only taking a stab at this. More of a closer approximation.

[Danny]

Lee, where's your popcorn eating little guy?

[mattawajeep]

Lee, where's your popcorn eating little guy?

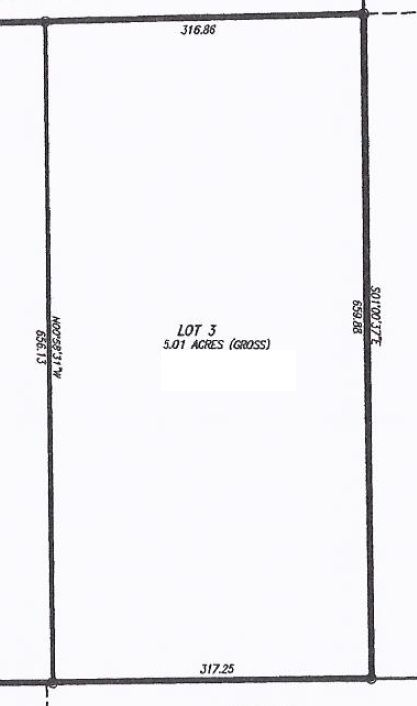
Pascoscout makes some good points, especially about rasterizing, or grabbing the bearing lines from the full plat. However, that isn't as entertaining.


I still don't think this is actually impossible, and I'll line out why.

I don't believe that a four sided polygon, even if it's not a rectangle or parallelogram, has an infinite number of solutions that can keep the same area. A five sided polygon would be another story.


So......

Take the polygon, pick a diagonal and make two triangles.

*Note, I have really exaggerated the angles here to make it clear nothing is parallel, and that the side lengths are different.



Note that we don't know diagonal C, and we also don't know how the area is split between the two triangles. However, we don't need to know that beforehand, as diagonal C is the same on both triangles, and that makes it solvable.






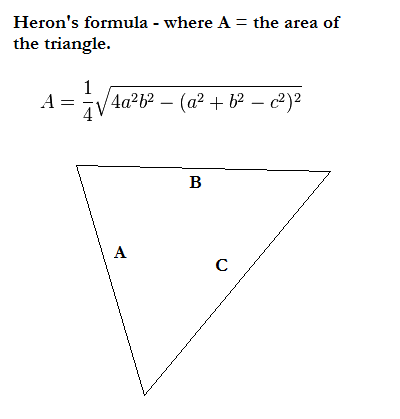
Once you plug in the numbers, and simplify things you end up with a quartic equation. What I was dumbly calling a quadratic to the 4th power. There are probably going to be two answers, but only one is real.

After sitting and thinking about this on the drive in to the meeting, I started remembering a bit of the old math. I think quartic equations that are not bi-quadratics were covered in the last week of math class, which I probably slept through.

I may look up how to solve the math part of this tomorrow. I think you end up using cubic formulas, but really don't remember well enough.


So what do you guys think? I'm I missing something glaringly obvious? Bored to tears?

[SPR]

I'm thinking no matter how accurately you place the your house on the plot drawing, in application, you may find it very difficult to locate the house on the dirt exactly as you planned without hiring a competent surveyor. An even then, it still may not workout as planned.

[iaccocca]

[mattawajeep]

I'm thinking no matter how accurately you place the your house on the plot drawing, in application, you may find it very difficult to locate the house on the dirt exactly as you planned without hiring a competent surveyor. An even then, it still may not workout as planned.

Yeah, I'm aware. Don't plan on using this for that, it's a foot off at most if I just draw a rectangle. The impossible seeming math problem was simply interesting, and when something stumps me I don't like to let it go.